Veke 13. Kostnadsoptimum
Grensekostnaden i optimum
14.4 Grensekostnaden i optimum
Eksempeloppgåve 14.9 Ei bedrift har kostnadsfunksjonen
Finn kostnadsoptimum. Rekn ut gjennomsnittskostnaden og grensekostnaden i kostnadsoptimum.
Løysing 14.4 Me må starta med gjennomsnittskostnadsfunksjonen
Optimum finn me ved å derivera:
Når me løyser likninga , får me
Kostnadsoptimumet er altso , og .
Me skisserer funksjonen for å dobbelsjekke at kostnadsoptimumet faktisk er et minimum.
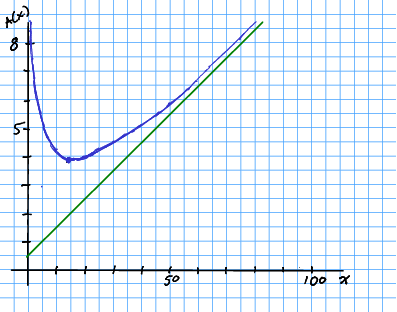
Me treng òg grensekostnaden
Verdiane i kostnadsoptimum er
Øvingsoppgåve 14.10 Ei bedrift har kostnadsfunksjonen
Finn kostnadsoptimum. Rekn ut gjennomsnittskostnaden og grensekostnaden i kostnadsoptimum.
Merknad 14.3 I desse oppgåvene var grense- og gjennomsnittskostnadene like i kostnadsoptimum. Når me ser slike «samantreff» lønar det seg å spørsja om det alltid er slik, og evt. kvifor det er slik.
Der finst eit algebraisk argument, men det konseptuelle argumentet er mest interessant.
Lat oss tenkja oss at prisen akkurat dekkjer gjennomsnittskostnaden i optimum og at prisen er konstant. Då går bedrifta akkurat i balanse. Dersom bedrifta endrar produksjonsvolumet frå optimum, so vil gjennomsnittskostnaden auka og bedrifta gå med underskot. Det vil seia at bedrifta ikkje berre står i kostnadsoptimum, men òg i profittoptimum.
I profittoptimum, må grensekostnaden vera lik prisen. Dersom grensekostnaden var høgare enn prisen, ville ein tena meir ved å redusera produksjone, og dersom grensekostnaden var lågare, vore der gevinst i auka produksjon. Difor er grensekostnaden lik prisen, som var lik gjennomsnittskostnaden.
Merknad 14.4 Nokon studentar og nokon bøker bruker regelen for å finna kostnadsoptimum. Det funkar, men ein treng ikkje hugsa denne regelen. Den generelle metoden for å finna optimum ved hjelp av derivasjon () fungerer for alle funksjonar, ogso .
Øvingsoppgåve 14.11 Ei bedrift har kostnadsfunksjonen
Skisser funksjonen for gjennomsnittskostnaden og finn kostnadsoptimum. Samanlikn med forrige oppgåve og drøft kor mykje bedrifta bør produsera.