Veke 12. Den andrederiverte
Den deriverte av høgare orden
13.1 Den deriverte av høgare orden
Eksempeloppgåve 13.1 Me har funksjonen med den deriverte:
Drøft og skissér .
Løysing 13.1 Legg merke til at er ein funksjon. Drøfting av vert det same som drøfting av einkvan annan andregradsfunksjon. Dvs. at me kan derivera han, slik
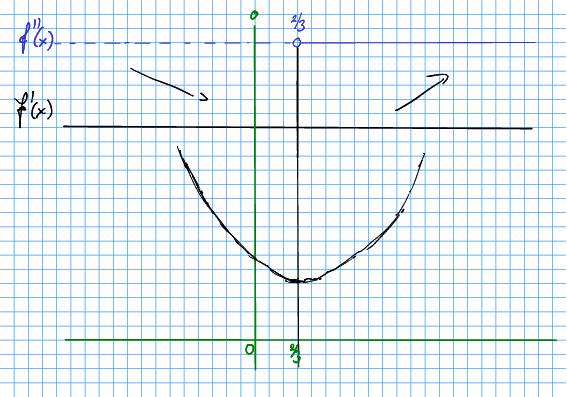
Me har for , og byter forteikn. Difor har eit ekstremalpunkt for .
Nullpunkta åt finn me med formel, som fylgjer
Her er inga løysing, so har ingen nullpunkt.
Me kan teikna forteiknsdiagram for og . Forteikna for viser at fyrst fell og so stig. Dette kan me bruka som utgangspunkt for å skissera som vanleg i koordinatsystemet.
Øvingsoppgåve 13.2 Me har funksjonen med den deriverte:
Drøft og skissér .
Merknad 13.1 Over har me funne den deriverte av den deriverte til ein funksjon . Funksjonen kallar me gjerne for den andrederiverte, eller den dobbelderiverte, av .
Eksempeloppgåve 13.3 Me har funksjonen med den deriverte:
Drøft og skissér .
Løysing 13.2 Me drøftar som einkvan annan tredjegradsfunksjon. Derivasjon gjev
Nullpunkt for er
Sidan andregradsleddet er positivt, har andregradsfunksjonen botnen ned. Då kan me teikna forteiknsdiagram, og skissera basert på det.
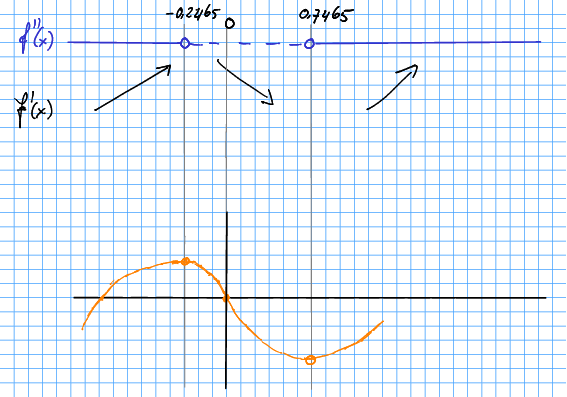
Me har markert nullpunkt i origo, sidan det er lett å sjå at alle ledda i er delelege med . Dei andre nullpunkta har me ikkje rekna ut.
Øvingsoppgåve 13.4 Me har funksjonen med den deriverte:
Drøft og skissér .