Veke 3–4. Eksponentialfunksjonen
Kontinuerleg forrenting
3.5 Kontinuerleg forrenting
Eksempeloppgåve 3.19 Sjå på eit lån med 10% nominell rente per år. Me har sett at lånet veks raskare di oftare forrentinga skjer. Kor ofte går det an å forrenta? Kva er den høgaste vekstfaktoren me kan få ved å forrenta uendeleg ofte.
Løysing 3.6 Sei at me har renteperiodar per år. Kvar periode vert lagt til lånet. Det svarer til ein vekstfaktor på
I løpet av året gongar me med vekstfaktoren gongar, slik at den samla vekstfaktoren vert
Lat oss sjå på nokre verdiar av og rekna ut med kalkulator.
| Frekvens | ||
| Årleg | 1 | 1,1 |
| Månadleg | 12 | 1,104 713 |
| Vekentleg | 52 | 1,105 065 |
| Dagleg | 365 | 1,105 156 |
| Kvar time | 8760 | 1,105 170 |
| Kvart minutt | 525 600 | 1,105 171 |
| Kvart sekund | 31 536 000 | 1,105 171 |
Øvingsoppgåve 3.20 Sjå på eit fond som veks med 100% nominell rente per år, og samanlikna ulike renteperiodar. Kva er den høgaste årlege vekstfaktoren du finn ved å forrenta uendeleg ofte?
Løysing 3.7 (Utfylling) Me har renteperiodar per år, og kvar gong legg med til eller på lånet. Det svarer til ein vekstfaktor på
Når me gangar med den same vekstfaktoren gongar, ver den samla vekstfaktoren
Fyll inn resten av tabellen med verdiar for
| Frekvens | ||
| Årleg | 1 | 2 |
| Månadleg | 12 | |
| Vekentleg | 52 | |
| Dagleg | 365 | |
| Kvar time | 8760 | |
| Kvart minutt | 525 600 | |
| Kvart sekund | 31 536 000 | 2,718 28 |
Merknad 3.2 Talet som me nærmar oss i løysinga over, har fått namnet , og . Formelt definerer me slik at når (når går mot uendeleg), so vil
dvs. går mot . I løysinga over har me funne korrekt verdi for med fem desimalar.
Øvingsoppgåve 3.21 Sjå på eit fond som veks med 20% nominell rente per år, og samanlikna ulike renteperiodar. Kva er den høgaste årlege vekstfaktoren du finn ved å forrenta uendeleg ofte?
Øvingsoppgåve 3.22 Aksjefondet Bravur har gått so det suser, med ei verdiauke på 250% per år. Tenk deg ulike periodiseringar av verdiauka. Kva er den høgaste årlege vekstfaktoren du finn ved å forrenta uendeleg ofte?
Merknad 3.3 Det som me har kalt «forrenting uendeleg ofte» i oppgåvene over, vert kalla kontinuerleg forrenting i fagspråket.
Eksempeloppgåve 3.23 Ved å gjenta oppgåvene over, kan me finna omtrentleg årleg vekstfaktor ved koninuerleg forrenting for ulike rentesatsar.
| Rentesats | Vekstfaktor |
| 300% | 20,086 |
| 200% | 7,389 |
| 100% | |
| 50% | 1,649 |
| 10% | 1,105 |
| 0% | 1 |
Plott samanhengen mellom rentesats og vekstfaktor. Korleis vil du beskriva denne samanhengen?
Løysing 3.8 Me kan teikna plottet for hand, og få:
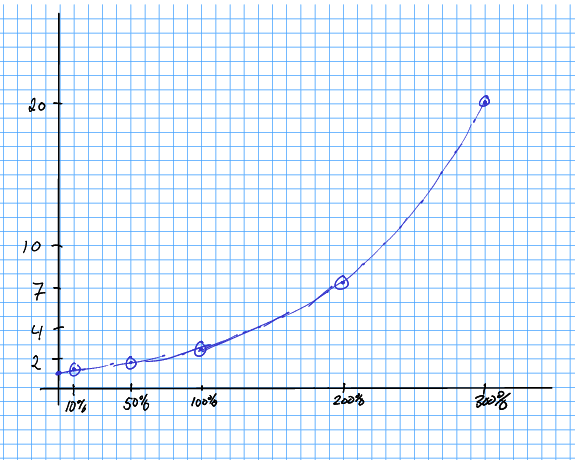
Denne kurva liknar på eksponentialfunksjonane som me har plotta i oppgåve 3.4. Dette ville ha vore enno tidlegare om me hadde teke med punkt for og større. Det er likevel naturleg å gissa på at vekstfaktoren er lik der er rentesatsen.
Øvingsoppgåve 3.24 I løysinga fremja me ein hypotese, om at årleg vekstfaktor ved kontinuerleg forrenting med rentesats , er gjeven som . Sjekk om denne samanhengen gjeld for dei vekstfaktorane som er rekna ut i oppgåve 3.23.
Løysing 3.9 (Utfylling)
| Rentesats | Vekstfaktor | Lik | ||
| 300% | 20,086 | 3 | 20,086 | Ja |
| 200% | 7,389 | 7,389 | ||
| 100% | ||||
| 50% | 1,649 | 0,5 | ||
| 10% | 1,105 | |||
| 0% | 1 | |||
Finn du noko tilfelle der ikkje er lik vekstfaktoren?
Merknad 3.4 Me legg merke til at me kan rekna ut potensen utan at er eit heiltal, i alle fall når me bruker kalkulator. Funksjonen er pen og glatt for alle ikkje-negative verdiar av og alle verdiar av .
Øvingsoppgåve 3.25 Sjekk om er riktig vekstfaktor for problema som du løyste i oppgåve 3.21 og 3.22.
Merknad 3.5 Når me har kontinuerleg forrenting med rentesats , so er samla årleg vekstfaktor lik .
Eksempeloppgåve 3.26 Ei investering på ein million kroner veks med kontinuerleg forrenting og rentesats i fem år. Kva er saldoen på slutten av kvart år i perioden?
Løysing 3.10 Lat oss setja det opp som ein tabell år for år. Vekstfaktoren er . Tala er i millionar kroner.
| År | Saldo |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
Øvingsoppgåve 3.27 Ei investering på 5000 kroner veks med kontinuerleg forrenting og rentesats i fem år. Kva er saldoen på slutten av kvart år i perioden?
Merknad 3.6 Merk at er den årlege vekstfaktoren ved kontinuerleg forrenting, og når fleire år går, gangar me (som vanleg) med same vekstfaktor for kvart år.
Øvingsoppgåve 3.28 Ei investering på 5000 kroner veks med kontinuerleg forrenting og rentesats . Kva er saldoen etter 2 år?
Merknad 3.7 Over har me funne ein formel for kontinuerleg forrenting. Når ein startkapital veks med kontinuerleg forrenting med rentesats , er kapitalen etter år gjeven som
Dette kan forenklast som
Dette fylgjer av potensreglane, men dei lyt ein slå opp andre plassar.