Veke 10. Modellering
Prisfunksjon
11.2 Prisfunksjon
Eksempeloppgåve 11.6 Me skal atter gå attende til bryggeriet frå oppgåve 8.18, der me fann profittfunksjonen
Lat oss no tenkja oss at prisen kan variera. Lat oss skriva for prisen i staden for 7, dvs.
Gjeve at bryggeriet går eksakt i balanse, skriv prisen som dei må krevja for ølet som ein funksjon av volumet .
Løysing 11.5 Me skal fram til eit uttrykk for . Føresetnaden om at bryggeriet går eksakt i balanse svarer til likninga , eller mao.
Denne likninga kan me løysa for , på vanleg måte, sjølv om vert ståande att som ein ukjend. Me må flytta over det eine leddet med , og få
No kan me dela med på båe sider,
Me ser no korleis avheng av . For å understreka at dette, kan me skriva med funksjonsnotasjon som . Prisfunksjonen er altso
når bryggeriet går i balanse.
Øvingsoppgåve 11.7 Lat oss gå tilbake til sandtaket på Mo i oppgåve 8.19. Kostnadsfunksjonen er . Inntektsfunksjonen hadde me funne som , men lat oss no tenkja at prisen er variabel, og ikkje konstant lik 600. Då er inntektsfunksjonen , og profittfunksjonen . Kva pris må sandtaket krevja for å gå i balanse? Skriv prisen som ein funksjon av produksjonsvolumet.
Eksempeloppgåve 11.8 I oppgåve 11.6 fann me ein prisfunksjon. I praksis er prisen normalt bestemt av marknaden, og bedrifta må tilpassa produksjonen til prisnivået. Profittfunksjonen er stadig
Finn ein produksjonsfunksjon som seier kor mykje bryggeriet kan produsera for eit gjeve prisnivå , medan drifta går i balanse.
Løysing 11.6 Utgangspunktet, om balanse i drifta, gjev likninga
I oppgåve 11.6 løyste me for . No skal me ha eit uttrykk for , og då må me løysa for .
Lat oss dra saman alle ledd med :
og flytta over konstandleddet:
Når me no deler på , får me eit uttrykk for :
Produksjonsfunksjonen er altso
når bryggeriet går i balanse.
Øvingsoppgåve 11.9 I oppgåve 11.7 fann me ein prisfunksjon. No ynskjer sandtaket å finna ut korleis dei skal tilpassa produksjonen til prisnivået som er sett av marknaden. Dei vil altso finna ein produksjonsfunksjon som seier kor mykje sand dei skal produsera dersom dei kan selja han for ein pris . Ta utgangspunkt i profittfunksjonen
og finn slik at .
Eksempeloppgåve 11.10 Ta pris- og produksjonsfunksjonane frå oppgåve 11.6 og 11.8:
Plott båe funksjonane.
Løysing 11.7 Legg merke til at og er produksjonsvolum i liter, medan og er pris i liter. Vanlegvis vil me ha funksjonsverdiane og på -aksen og argumenta og på -aksen. Då kan me ikkje plotta funksjonane i same diagram.
Korkje eller er lineære funksjonar, fordi variabelen (hhv. og ) står under brøkstreken. Då må me rekna ut litt meir enn to punkt for å teikna godt.
| 0 | −1428,57 |
| 2 | −2000,00 |
| 5 | −5000,0 |
| 6 | −10 000,0 |
| 8 | 10 000,0 |
| 9 | 5000,0 |
| 10 | 3333,33 |
| 15 | 1250,00 |
| 20 | 769,23 |
| 1 | 10 007,00 |
| 750 | 20,33 |
| 1250 | 15,00 |
| 2500 | 11,00 |
| 5000 | 9,00 |
| 10000 | 8,00 |
Me kan plotta punkta og dra ei kurve gjennom dei på frihand.
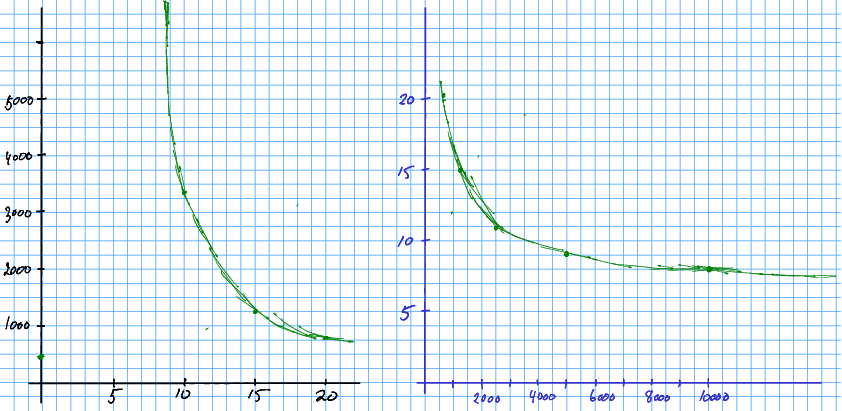
Øvingsoppgåve 11.11 Ta pris- og produksjonsfunksjonane som du fann i oppgåve 11.7 og 11.9 og plott dei i eit rutenett.
Merknad 11.1 Me har funne to funksjonar (oppgåve 11.6) og (oppgåve 11.8). Dei to er inverse funksjonar. Den eine reknar frå pris til produksjonsvolum, og den andre reknar tilbake.
Merknad 11.2 Dei to funksjonane
er døme på rasjonale funksjonar. Det ser fordi variabelen (hhv. og dukkar opp under brøkstreken).
Kravet til ein rasjonal funksjon er at han kan skrivast som ein brøk med polynom over og under streken. Dette ser me umiddelbart for , medan kan skrivast om som ein brøk for å tydleggjera det: