Veke 8. Kvadratiske kostnadsfunksjonar
Introduksjon
9.1 Introduksjon
Eksempeloppgåve 9.1 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
som gjev samla produksjonskostnad når dei produserer einingar, forutsett at . Skisser kostnadsfunksjonen i eit koordinatsystem.
Løysing 9.1 Når funksjonen ikkje er lineær, treng me nokre forskjellige punkt for å finna formen. Lat oss tabulera fyrst.
| 50 | 25 |
| 100 | 50 |
| 200 | 250 |
| 300 | 650 |
| 400 | 1250 |
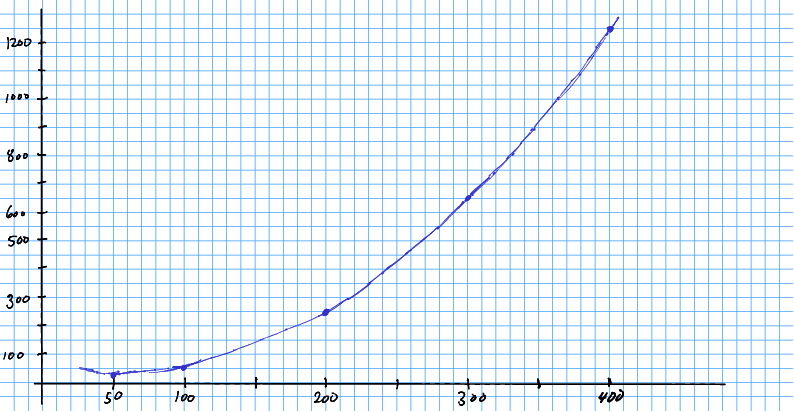
Øvingsoppgåve 9.2 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
som gjev samla produksjonskostnad når dei produserer einingar. (Me føreset at .) Skisser kostnadsfunksjonen i eit koordinatsystem.
Merknad 9.1 Kostnadsfunksjonane over er døme på kvadratiske funksjonar, eller andregradsfunksjonar som dei òg vert kalt. Ein kvadratisk funksjon har formen
Når me plottar ein kvadratisk funksjon, får me ein form som vert kalt ein parabel, men denne formen kjem ikkje skikkeleg til syne i løysingane over, fordi me ikkje viser negative verdiar av .
Eksempeloppgåve 9.3 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
som gjev samla produksjonskostnad når dei produserer einingar, forutsett at .
- 1.
- Sett at bedrifta produserer einingar. Kor mykje ekstra kostar det å auka produksjonen til 101?
- 2.
- Sett at bedrifta produserer einingar. Kor mykje ekstra kostar det å auka produksjonen til 501?
Løysing 9.2 Lat oss rekna ut kostnaden for dei ulike produksjonsvoluma. Me skriv for kostnadsendringa.
| 100 | 101 | 51,01 | 50 | 1,01 |
| 500 | 501 | 2059,01 | 2050 | 9,01 |
Det kostar altso kr. 1,01 å auka produksjonen frå 100 til 101, og kr. 9,01 frå 500 til 501.
Merknad 9.2 Med lineære kostnadsfunksjonen hadde me variable kostnader som utgjorde eit fast beløp per produsert eining. Det er interessant å sjå at dette ikkje er tilfelle med kvadratiske funksjonar.
Øvingsoppgåve 9.4 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
som gjev samla produksjonskostnad når dei produserer einingar. (Me føreset at .)
- 1.
- Sett at bedrifta produserer einingar. Kor mykje ekstra kostar det å auka produksjonen til 21?
- 2.
- Sett at bedrifta produserer einingar. Kor mykje ekstra kostar det å auka produksjonen til 41?