Veke 8. Kvadratiske kostnadsfunksjonar

Eksempeloppgåve 9.11 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:

som gjev samla produksjonskostnad når dei produserer $x$ einingar, forutsett at $x\ge 10$. Bedrifta sel produktet for 200 kroner per eining. Kor mykje må dei produsera for å gå med overskot?

Løysing 9.6 Me må fyrst finna profittfunksjonen. Inntektsfunksjonen er $I\left(x\right)=200x$, og profittfunksjonen vert då

Når me løyser opp parentesane, får me

Dei to fyrstegradsledda ($200x$ og $-100x$) kan me slå saman, og skriva

Me skal finna dei $x$-verdiane som gjev overskot, dvs. $P\left(x\right)>0$. Dette er ein ulikskap.

Lat oss fyrst finna nullpunkta, $P\left(x\right)=0$, der bedrifta går i balanse. Me bruker formelen med $a=-1∕100$, $b=100$ og $c=500$.

Dersom me gongar med $-50$ over og under streken, får me

Med litt hjelp av kalkulator, får me

Lat oss no skissera funksjonen for å sjå kvar profitten er positiv.

Løysinga av andregradslikninga fortel oss at profittfunksjonen kryssar $x$-aksen to gongar, for $x=\text{10 005,0}$ og for $x=\text{−5,0}$. Me kan merka dei to punkta fyrst.

Det neste me skal merka oss er at når $x$ vert svært stor ($x\to \infty$), so veks $x^2∕100$ mykje raskare enn $100x$, og $x^2∕100$ har negativt forteikn. Difor har me $P\left(x\right)\to -\infty$ når $x\to \infty$. Det same skjer når $x\to -\infty$. Me har altso underskot både til venstre for $\text{−5,0}$ og til høgre for $\text{10 005,0}$.

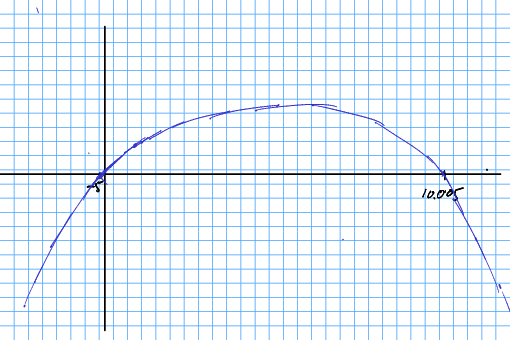
Sidan me veit korleis ein parabel ser ut, veit me at $P\left(x\right)$ byter forteikn i nullpunkta. Alternativt, om me er i tvil, kan me sjekka ein verdi mellom nullpunkta. Det plar vera lett å sjekka for $x=0$; me får $P\left(x=0\right)=500$.

No skal me hugsa at kostnadsfunksjonen for bedrifta berre var definert for $x\ge 10$. Dermed fylgjer det at bedrifta går med overskot for $10\le x<\text{10 005,0}$.

Øvingsoppgåve 9.12 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:

som gjev samla produksjonskostnad når dei produserer $x$ einingar. Bedrifta sel produktet for 18 kroner per eining. Kor mykje må dei produsera for å gå med overskot?