Veke 11. Funksjonsdrøfting

Eksempeloppgåve 12.1 Drøft og skissér funksjonen

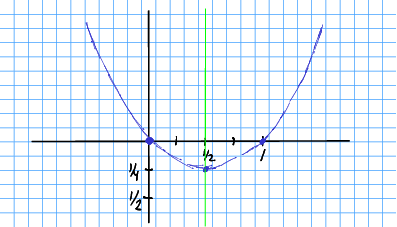
Løysing 12.1 Det er greitt å ha med skjæringspunkta med aksane. Me kan sjå (ved å trekkja ein $x$ utanfor parentes) at

Dermed har me to nullpunkt, eitt for kvar faktor, når $x=0$ og når $x-1=0$.

Me veit at andregradsfunksjonen er symmetrisk, og symmetrilina går midt mellom nullpunkta, altso for $x=\frac{1}{2}$.

For å finna $y$-verdien i ekstremalpunktet, som ligg på symmetrilina, set me inn i funksjonen:

Dette er nok informasjon til å fullføra skissa.

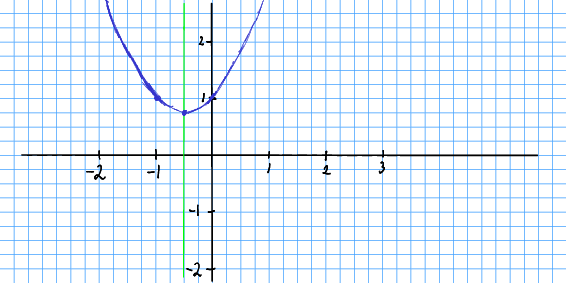
Øvingsoppgåve 12.2 Drøft og skissér funksjonen

Eksempeloppgåve 12.3 Drøft og skissér funksjonen

Løysing 12.2 Det er greitt å ha med skjæringspunkta med aksane. Nullpunkta finn me ved å løysa likninga $f\left(x\right)=0$. Formelen for andregradslikningar gjev

Legg merkje til $-3$ under rotteiknet. Kvadratrota er ikkje definert for negative tal, og difor har funksjonen ingen nullpunkt.

Me kan finna botnpunktet ved å derivera:

og $f^{\prime }\left(x\right)=0$ for $x=-\frac{1}{2}$. Funksjonen er altso symmetrisk om lina $x=-\frac{1}{2}$, og funksjonsverdien i botnpunktet er

Dette er eit godt utgangspunkt for å skissera.

Øvingsoppgåve 12.4 Drøft og skissér funksjonen

Øvingsoppgåve 12.5 Drøft og skissér funksjonen

Øvingsoppgåve 12.6 Drøft og skissér funksjonen

Merknad 12.2 Der er ein symmetri i formelen for å løysa andregradslikningar:

Der er to røter, éi for positivt og éi for negativ rottuttrykk. Røtene ligg symmetrisk om lina

Me kan alltid finna symmetrilina på denne måten, og me ser at det ville ha gjeve same svar i løysinga på oppgåve 12.3.