Veke 12. Den andrederiverte
Vendepunktet
13.3 Vendepunktet
Eksempeloppgåve 13.9 Sjå på funksjonen . Denne funksjonen har eit lokalt maksimum for og lokalt minimum for . Sjå på kurva på intervallet . Kvar er ho brattast?
Løysing 13.5 Lat oss plotta i full fart.
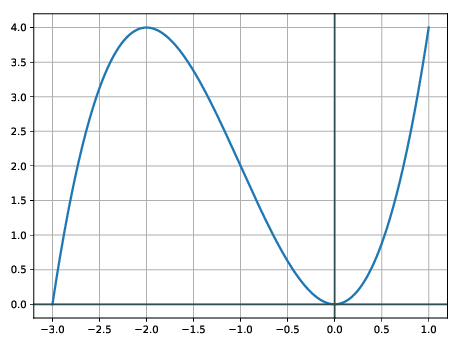
Kurva er openbert slak nær ekstremalpunkta. Det ser ut som om ho er brattast midt mellom topp- og botnpunktet, altso ved , men for å vera sikker på at svaret er nøyaktig er det best å bruka algebra.
Målet for bratte er stigningstalet åt tangenten, altso den deriverte:
Me veit allereie frå oppgåva og plottet at og at for , men kvar er minst (mest negativ)?
For å finna minimumspunktet åt , deriverer me igjen
Me ser at . Dette er altso minimumspunktet åt og det brattaste punktet nedover på . Dette punktet vert òg kalla vendepunktet åt .
Merknad 13.2 (Vendepunkt) I figuren ser me korleis kurva krummar med hulsida ned til venstre for vendepunktet og hulsida opp til høgre for vendepunktet. Den andrederiverte byter forteikn i vendepunktet. Han er negativ til venstre, der vert mindre og mindre og lagar hulside ned på . Han er positiv til høgre, der vert større og lagar hulside opp på .
Øvingsoppgåve 13.10 Sjå på funksjonen . Denne funksjonen har eit lokalt maksimum for og lokalt minimum for . Sjå på kurva på intervallet . Kvar er ho brattast?
Løysing 13.6 Me finn den deriverte
Nullpunkta åt finn me med formelen for andregradslikningar
Dette er ekstremalpunkta åt .
Me kan finna vendepunktet ved å setja den andrederivert lik null:
Me løyser likninga
Me kan finna funksjonsverdien i dei tre interessante punkta:
Då har me fylgjande plott.
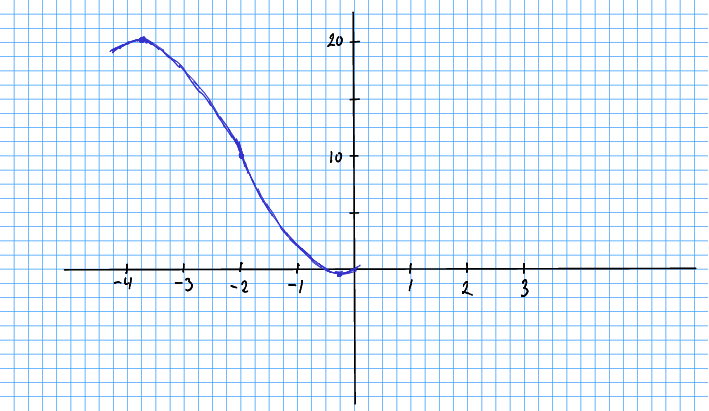
Øvingsoppgåve 13.12 Drøft og skisser funksjonen . Marker vendepunktet med - og -verdi.