Veke 7. Lineær kostnad og inntekt
Lina gjennom to punkt
8.5 Lina gjennom to punkt
Eksempeloppgåve 8.26 Hansens slakteri slakta 12.000 sauar i 2017. Dette gav totale produksjonskostnader på åtte millionar kroner. Dei estimerer at den variable kostnaden per sau levert frå slakteriet er 500 kroner, og går ut frå at kostnadsfunksjonen er lineær. Teikn kostnadsfunksjonen i eit rutenett.
Løysing 8.11 Me kjenner eit punkt i plottet, kostnaden på 8 mill. kr. for 12 000 sauar. Det er det fyrste punktet me plottar.
Dersom me aukar produksjonen med 1000 sauar til 500 kroner per stykk, aukar kostnaden med ein halv million. Denne endringa kan me teikna som eit kort linestykke. Likeeins, dersom ein reduserer produksjonen med 1000 sauar, går kostnaden ned med ein halv million.
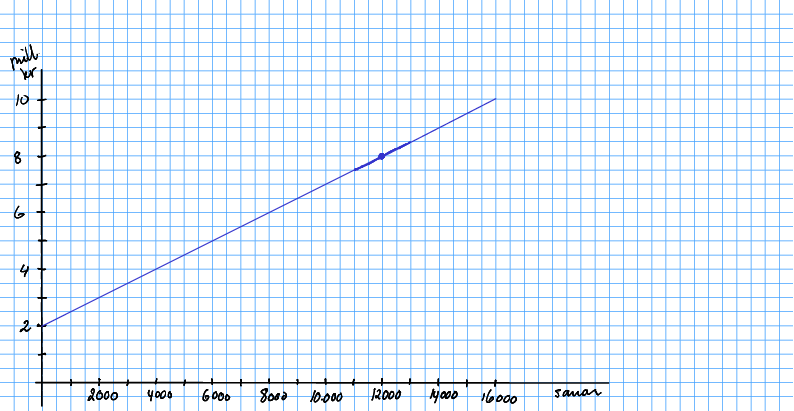
Sidan ekstrakostnaden per sau er konstant, kan me forlengja lina med konstant stigningstal.
Merknad 8.6 Legg merke til at årstalet 2017 er irrelevant for løysinga. Det speler inga rolle når slakteriet observerte produksjonskostnaden. Den typen «støy» i oppgåveteksta må ein øva seg til å handtera, fordi slik støy og overflødig informasjon er ein del av livet.
Her er ein video til ettertanke: https://www.youtube.com/watch?v=kibaFBgaPx4.
Øvingsoppgåve 8.27 Kari er konditor og sel kaker. Kvar kake kostar 60 kroner i råvarer. I januar produserte Kari 400 kaker og hadde samla kostnader på 38 000 når husleige, løn til lærlingen og alt anna er medrekna. Teikn kostnadsfunksjonen i eit rutenett.
Eksempeloppgåve 8.28 Hansens slakteri slakta 12.000 sauar i 2017. Dette gav totale produksjonskostnader på åtte millionar kroner. Dei estimerer at dei variable kostnaden per sau levert frå slakteriet er 500 kroner, og går ut frå at kostnadsfunksjonen er lineær. Finn eit uttrykk for kostnadsfunksjonen.
Løysing 8.12 (Faste og variable kostnader) Her er det mange opplysingar, so me må strukturera dei litt. Det er fornuftig å starta med ein matematisk form for svaret som me skal fram til, altso ein lineær kostnadsfunksjon, som ser slik ut:
Her er den variable kostnaden per sau, og er dei faste kostnadene. Lat oss seia at og er målte i kroner.
Dei variable kostnadene er gjevne i oppgåva som . Den faste kostnaden er ukjend, men me veit at kostaden for 12.000 sauar kan skrivast som
Då ser me at dei variable kostnadene for 12.000 sauar er
Sidan dei totale kostnadene er åtte millionar, må dei fast kostnadene vera to millionar, og me kan skriva
Øvingsoppgåve 8.29 Kari er konditor og sel kaker. Kvar kake kostar 60 kroner i råvarer. I januar produserte Kari 400 kaker og hadde samla kostnader på 38 000 når husleige, løn til lærlingen og alt anna er medrekna. Finn eit uttrykk for kostnadsfunksjonen.
Eksempeloppgåve 8.30 Dingsemakaren har erfart at produksjonskostnadene er 20.000 kroner i ein månad der han produserer 200 dingsar. Når han produserer 300 dingsar per månad, er produksjonskostnadene 25.000 kroner. Me går ut frå at kostnadsfunksjonen er lineær. Kva er dei variable kostnadene per dings?
Løysing 8.13 Me skal finna dei variable kostnadene. Då kan me ta utgangspunkt i variasjonen mellom dei to produksjonsvoluma som er kjende.
| Volum | Kostnad | |
| Andre fall | 300 | 25.000 |
| Fyrste fall | 200 | 20.000 |
| Skilnad | 100 | 5.000 |
Ei auke på 100 dingsar kostar altso 5000 kroner, eller 50 kroner per dings.
Øvingsoppgåve 8.31 Skomakar Hagen kan produsera 25 par sko på ein månad til ein samla kostnad på 16.000 kroner. Han kan klara 30 par sko til ein kostnad på 18.000 kroner. Me går ut frå at kostnadsfunksjonen er lineær. Kva er dei variable kostnadene per skopar?
Eksempeloppgåve 8.32 Dingsemakaren har erfart at produksjonskostnadene er 20.000 kroner i ein månad der han produserer 200 dingsar. Når han produserer 300 dingsar per månad, er produksjonskostnadene 25.000 kroner.
- 1.
- Plott dei to kostnadsdøma i eit koordinatsystem, og teikn ei rett line gjennom punkta.
- 2.
- Finn ein lineær kostnadsfunksjon som passar med kostnadsdøma.
- 3.
- Me kan lesa lina i plottet som ein funksjon. Samanlikn han med kostnadsfunksjonen i pkt. 2. Er det same funksjon?
Løysing 8.14 Plottet er rett fram å teikna:
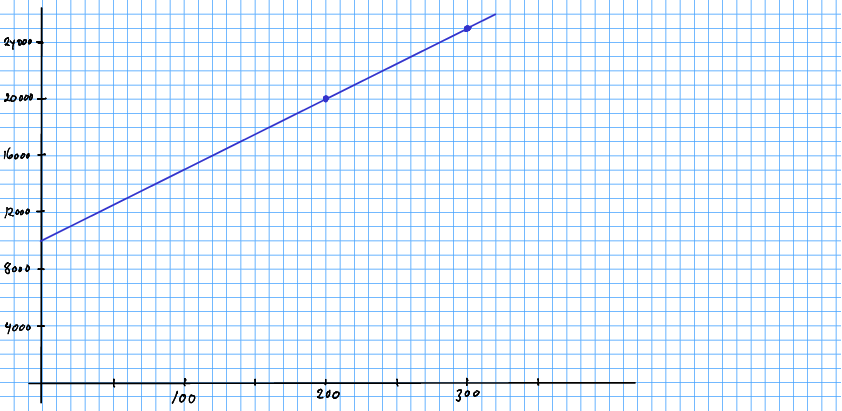
Me ser at kostnaden aukar med 5000 kroner når produksjonen aukar med 100 dingsar. Det gjev ei auke på 50 kroner/dings. Dette er den variable kostnaden, eller stigningstalet på funksjonen, og kostnadsfunksjonen må altso vera for ein eller annan faste kostnad .
For 200 dingsar utgjer dei variable kostnadene kroner, utav 20000 kroner i totale kostnader. Dvs. at dei faste kostnadene må vera 10000 kroner. Kostnadsfunksjonen er då
I plottet ser me at lina kryssar -aksen ved 10 000 kroner. Det er kostnaden ved nullproduksjon som me ser stemmer med konstantleddet i . Me kan òg sjå at stigningstalet er 50, eller 5000 kroner per 100 dingsar, både i plottet og i funksjonsuttrykket.
Figuren er eit plott av .
Øvingsoppgåve 8.33 Skomakar Hagen kan produsera 25 par sko på ein månad til ein samla kostnad på 16.000 kroner. Han kan klara 30 par sko til ein kostnad på 18.000 kroner
- 1.
- Plott dei to kostnadsdøma i eit koordinatsystem, og teikn ei rett line gjennom punkta.
- 2.
- Finn ein lineær kostnadsfunksjon som passar med kostnadsdøma.
- 3.
- Me kan lesa lina i plottet som ein funksjon. Samanlikn han med kostnadsfunksjon i pkt. 2. Er det same funksjon?
Øvingsoppgåve 8.34 (Abstrakt) Ei line går gjennom punkta og i eit koordinatsystem. Finn ein funksjon som beskriv lina.