Veke 9. Grensekostnad
Topp- og botnpunkt
10.3 Topp- og botnpunkt
Eksempeloppgåve 10.13 Ålesund Dings og Profitt AS har rekna ut at dei har profittfunksjonen
for produserte og solgte dingsar. Bedrifta ynskjer å maksimera profitten. Kor mange dingsar bør dei produsera og selja?
Løysing 10.7 Lat oss teikna ei skisse i full fart, for å sjå kva me arbeider med. Her har me teikna på maskin, som ei avveksling.
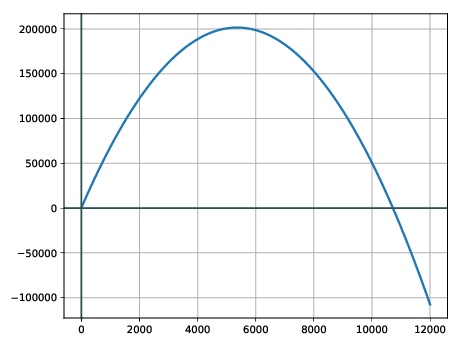
Lat oss tenkja over kva som skjer med den deriverte når produksjonen aukar. Profittkurva går fyrst oppover, dvs. positivt stigningstal, og . Kurva flatar ut, som vil seia at stigningstalet vert mindre. På toppen går den deriverte frå å vera positiv, til å verta negativ. Mot høgre vert kurva brattare og brattare nedover, som vil seia at den deriverte vert svært negativ.
Akkurat på toppen, når den deriverte går frå positiv til negativ, er der eitt punkt der den deriverte er null. Det er toppunktet, beste moglege profitt, og det skal me finna. Me skal altso løysa likninga .
Lat oss fyrst derivera
Veksta skulle vera null, so me får likninga
Når me løyser, får me
Det er ok å skriva at svaret er .
Er me litt grundigare, hugsar me at dingsar ikkje kan delast opp. Svaret skulle difor vera anten 5357 eller 5358. Lat oss sjekka kva som er best
Det optimale er altso å produsera 5357 dingsar.
Øvingsoppgåve 10.14 Ørsta Fisk og Profitt AS har rekna ut at dei har profittfunksjonen
for produserte og solgte dingsar. Bedrifta ynskjer å maksimera profitten. Kor mange dingsar bør dei produsera og selja?
Øvingsoppgåve 10.15 Ta funksjonen
Finn minimumspunktet, dvs. den -verdien som gjev minst verdi for .
Øvingsoppgåve 10.16 Ta funksjonen
- 1.
- Har eit topp- eller botnpunkt?
- 2.
- Finn optimum (topp- eller botnpunkt).