Veke 9. Grensekostnad
Derivasjon
10.4 Derivasjon
Eksempeloppgåve 10.17 Ein funksjon definerer fylgjande kurve:
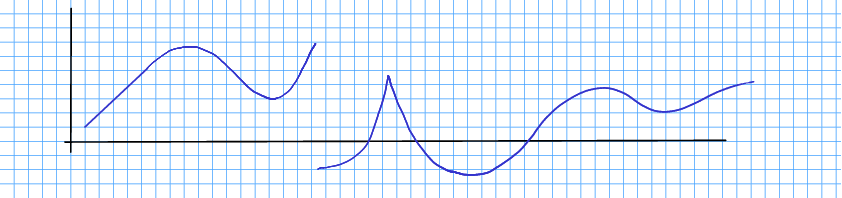
Skissér kurva for den deriverte, .
Løysing 10.8 Me merker oss fleire distinkte punkt på kurva, og dei bør me merka av fyrst.
- 1.
- Kurva er diskontinerleg (1).
- 2.
- Kurva har eit knekkpunkt (2).
- 3.
- Kurva har eit slags knekkpunkt (3), der ho fyrst er lineær og so flater ut.
- 4.
- Fem topp- og botnpunkt (4-8).
I alle topp- og botnpunkta er den deriverte null, so dette kan me merka av fyrst. Me bruker raudt for den deriverte og blått for den opprinnelege funksjonen.
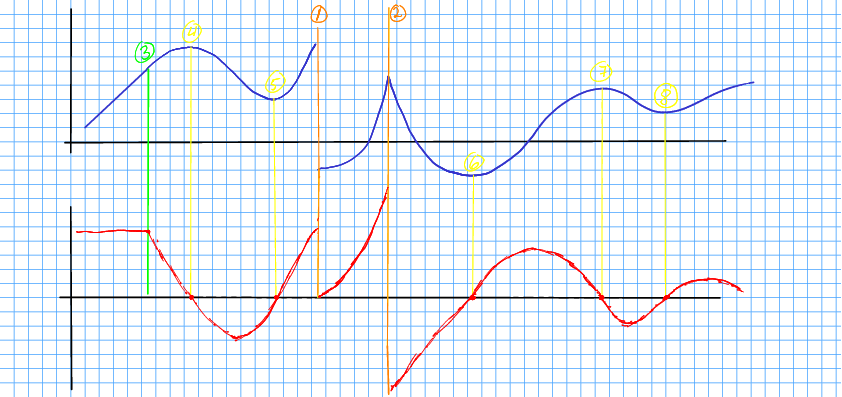
Der kurva er lineær, er stigningstalet og dermed den deriverte, konstant. Me kan altso teikna ei flat line til venstre for den grøne lina (3). Kurva stig, so den deriverte er positiv.
Til venstre for den grøne lina vert stigninga mindre ned mot null ved den gule lina (4) og vert negativ. Han snur og kryssar -aksen ved den gule lina (5), og endar positiv ved diskontinuiteten (1).
Mellom dei oransje linene, startar den deriverte cirka på null, og stigningtalet stig. Ved knekkpunktet (2) går kurva brått frå å stiga til å falla, so den deriverte vert diskontinuerleg og held fram under -aksen.
Det siste stykket er relativt enkelt å teikna. me må treffa nullpunkta som svarer til topp- og botnpunkt, og me freistar å teikna ein stor verdi for den deriverte når kurva er bratt, men det går best på augemål.
Øvingsoppgåve 10.18 Ein funksjon definerer fylgjande kurve:
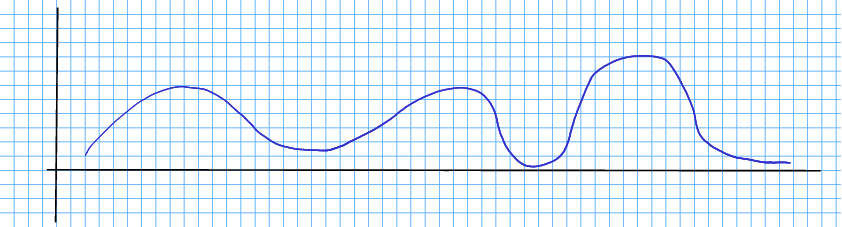
Skissér kurva for den deriverte, .
Øvingsoppgåve 10.19 Ein funksjon definerer fylgjande kurve:
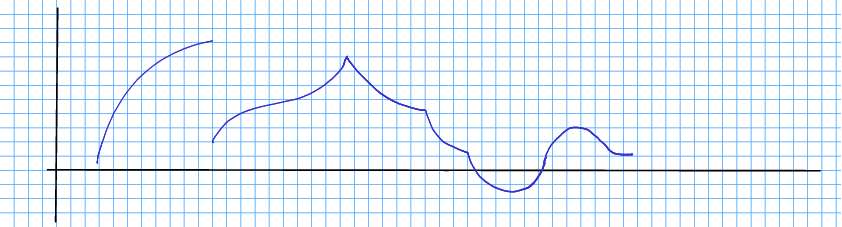
Skissér kurva for den deriverte, .
Øvingsoppgåve 10.20 Ein funksjon definerer fylgjande kurve:
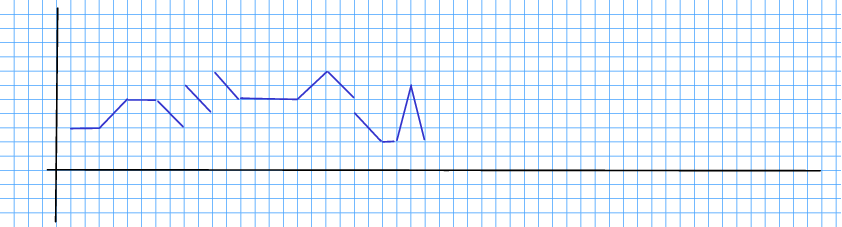
Skissér kurva for den deriverte, .
Øvingsoppgåve 10.21 Sjå på funksjonen
Plott funksjonen, for hand eller på maskin. Skisser deretter den deriverte, , basert på kva du ser i plottet av .
Øvingsoppgåve 10.22 Sjå på funksjonen
Plott funksjonen, for hand eller på maskin. Skisser deretter den deriverte, , basert på kva du ser i plottet av .