Fleire døme
Matematikk frå Røynda
7 Fleire døme
Desse oppgåvene vart gjevne som obligatorisk arbeidskrav i 2018. Dei er stadig relevante og eg vil råda dykk til å freista å løysa dei når de er ferdige med resten av heftet, og bruka løysingsforslaga som fasit om det trengst.
Eksempeloppgåve 7.1 Snorre og Synnøve har arva ein millon kroner kvar og set pengane i aksjefond. Snorre vel eit lågrisikofond og får 1,5% rente (avkasting) per år. Synnøve vel høgare risiko, og har flaks; ho får 2,5% rente.
- 1.
- Plott verdiutviklinga for både Snorre og Synnøve i same koordinatsystem frå innskotstidspunktet og femti år fram i tid.
- 2.
- Kor lang tid tek det før Snorre har fått dobla verdien?
- 3.
- Kor lang tid tek det før Synnøve har fått dobla verdien?
Løysing 7.1 Saldoen hennar Synnøve (i millionar kroner) kan skrivas som
der er tida i år. Tilsvarande er saldoen hans Snorre
Me plottar båe funksjonane ved å rekna ut saldoen for år.
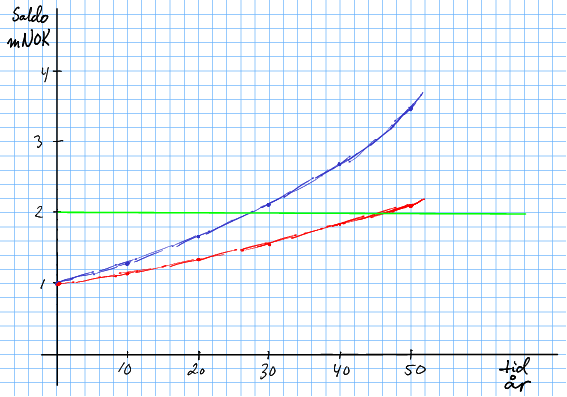
Me ser på augemål at Snorre doblar saldoen etter cirka 45 år, og Synnøve etter rundt 27 år. For å finna nøyaktige tal, må me derimot løysa likninga for Synnøve og for Snorre.
For Synnøve har me då
Det tek altso litt meir enn 28 år før Synnøve har dobla saldoen. Plottet er med andre ord ikkje heilt presist, men det er akseptabelt.
For Snorre har me
Det tek altso litt cirka 45 år før Snorre har dobla saldoen. Igjen er plottet litt upresist men akseptabelt.
Merknad 7.1 Denne oppgåva gjev ein del tolkingsrom i korleis ein skal svara. Rådet er då å bruka både plottet og algebraen for å dobbelsjekka svaret, og styrka presentasjonen.
Oppgåva er definitivt relevant som eksamensoppgåve, men formuleringa vil normalt vera litt meir presis på eksamen.
Eksempeloppgåve 7.2 Du får tilbod om eit lån til 3% nominell rente per år, med månadleg forrenting. Der er ingen gebyr. Kva er den effektive rentesatsen?
Løysing 7.2 Rentesatsen på 3% per år, gjev rente per månad. Med månadleg forrenting, vert vekstfaktoren 1,0025 på ein månad. Over tolv månader vert vekstfaktoren
som svarer til ein effektiv rentesats på per år.
Merknad 7.2 Dette problemet kan dukka opp på eksamen, sjølv om ein ikkje tidlegare har spurt om effektiv rentesats. Då kan ein rekna med at effektiv rente vert definert i oppgåva, men teknikken må ein kunna.
Eksempeloppgåve 7.3 Politikarane debatterer ny hovudveg, som evt. kan byggjast 2022–24. Kostnaden er venta å verta éin milliard kroner kvart år i byggjeperioden på tre år. Diskonteringsrenta er 4%. Rekn ut noverdien (per 2018) av dette prosjektet.
Løysing 7.3 Kostnaden omfattar tre beløp, om fire, fem og seks år. Me kan setja dei opp i ein tabell
| År | Nominelt | Noverdi |
| 2022 | 1 | |
| 2023 | 1 | |
| 2024 | 1 | |
| Sum | ||
Noverdien av prosjektet er altso 2,467 milliardar kroner.
Merknad 7.3 Ein kan godt setja dette opp som ei geometrisk rekkje, men me berre tre ledd er gevinsten liten. Det beste er å bruka den teknikken som ein er tryggast på.
Merknad 7.4 Slike oppgåver kan dukka opp på eksamen, sjølv om det vil vera meir vanleg med oppgåver med fleire ledd i summen, slik at ein må setja det opp som ei geometrisk rekkje og bruka formel.
Eksempeloppgåve 7.4 Anne Sofie har 20 000 kr. i eit aksjefond. Ved slutten av kvart år får ho 5% avkasting og tek ut 1000 kr. Kor mange år går det før ho har brukt opp pengane?
Løysing 7.4 Avkastinga er kroner. Når ho tek ut 1000 kroner svarer det akkurat til avkastinga, og saldoen vert stabil på 20 000 kroner. Pengane hennar varer altso evig.
Merknad 7.5 Ein kan godt setja dette opp algebraisk (vha. ei geometrisk rekkje) og sjå at ein får divisjon med null. So snart ein ser at ho berre tek ut rentane, er derimot presentasjonen over enklare å skriva og enklare å forstå. Det enklaste er ofte det beste.
Merknad 7.6 Dette er kan vera ei eksamensoppgåve, sjølv om det er meir vanleg med ein variant der pengane vert brukte opp og svaret ikkje er uendeleg.
Eksempeloppgåve 7.5 Filip vurderer å kjøpa opp ei lita bedrift. Han trur at bedrifta har eit unikt konsept som vil gje 500 000 kroner i profitt kvart år i all framtid. Han reknar med ei diskonteringsrente på 3%. Kor mykje er han maksimalt viljug til å betala for bedrifta?
Løysing 7.5 Her er me interessert i kontantstraumen på million kroner per år, diskontert med 3% rente per år. Lat oss gå ut frå at den fyrste utbetalinga kjem umiddelbart. Det gjev den geometriske rekkja
Der er noverdien i millioner kroner. Her kan me bruka formelen for geometriske rekkjer:
Filip kan altso by inntil 17,167 millioner kroner utan å forventa tap.
Det er kanskje meir realistisk at den fyrste utbetalinga kjem om eitt år, og ikkje umiddelbart. Det forskyver heile kontantstraumen eitt år ut i framtida, og noverdien vert millionar kroner. Oppgåvå skriv ikkje når utbetalingane tek til.
Merknad 7.7 Mange vil lika å skriva rekkja med summeteikn
Det kan vera fornuftig, men det er viktig å understrekja at det berre er notasjon og får oss ikkje nærare ei løysing. Mao. det er smak og behag.
Merknad 7.8 Løysinga har gjeve to svar med ulik føresetnad. Det gjer ein gjerne i eit absolutt perfekt svar. Det er likevel fullstendig og korrekt å velja éin føresetnad og gje eitt svar. Oppgåva skriv ikkje når utbetalingane tek til, og ein står fritt til å velja. Valet bør kommenterast, men det er ein detalj.
Merknad 7.9 Dette er ei ganske typisk eksamensoppgåve.