Kvadratiske kostnadsfunksjonar
Balanse: den kvadratiske likninga
2.2 Balanse: den kvadratiske likninga
Når ei likning er gjeve som
er løysinga gjeve som
Dersom uttrykket er negativt, er rotuttrykket ikkje definert og likninga har inga løysing.
Formen (10) kan me kalla for standardformen for ei andregradslikning.
Eksempeloppgåve 2.5 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
Kostnadsfunksjonen gjev samla produksjonskostnad når dei produserer einingar, forutsett at . Bedrifta sel produktet for ei krone per eining. Kor mykje skal dei produsera og selja for å gå akkurat i balanse?
Løysing 2.3 Me har berre fått oppgjeve kostnadsfunksjonen og ikkje inntektsfunksjonen . Me har derimot prisen , so me kan skriva
Balansepunktet er gjeve som , eller
Dette er ei andregradslikning sidan alle ledda er anten konstante (uavhengige av ), eller ein konstant gonga med eller . Likninga er derimot ikkje på standardform, og me må rydda opp før me kan bruka formelen (Rekneregel 2.1).
Me trekk frå på båe sider av likninga og får
Me kan òg setja utanfor brøken:
No er det lett å sjå at me har standardformen med , og .
Innsetjing gjev
Me kan rekna ut dei ulike ledda og få
eller
Dette gjev to nullpunkt, og , men oppgåva føreset for at kostnadsfunksjonen skal vera gyldig, so berre den siste løysinga er gyldig.
Bedrifta går i balanse når dei produserer liter.
Øvingsoppgåve 2.6 Lat oss tenkja oss ei bedrift med fylgjande kostnadsfunksjon:
som gjev samla produksjonskostnad når dei produserer einingar. Bedrifta sel produktet for 80 kroner per eining. Kor mykje skal dei produsera og selja for å gå akkurat i balanse?
Eksempeloppgåve 2.7 Plott inntekts- og kostnadsfunksjonane frå oppgåve 2.5. Finn punktet der drifta går i balanse og samanlikn med løysinga som du fann i oppgåve 2.5.
Løysing 2.4 Det enklaste og tryggaste er å tabulera funksjonsverdiane for nokre verdiar av . Merk at me ikkje ser på , sidan kostnadsfunksjonen ikkje er gyldig for små verdiar av .
| 50 | 25 | 50 |
| 100 | 50 | 100 |
| 200 | 250 | 200 |
| 300 | 650 | 300 |
| 400 | 1250 | 400 |
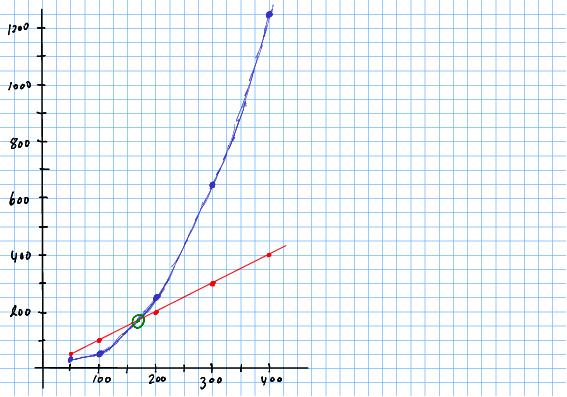
Me finn skjæringspunktet der kostnadene er lik inntekta, ved som stemmer godt med rekninga vår tidlegare.
Øvingsoppgåve 2.8 Plott inntekts- og kostnadsfunksjonane frå oppgåve 2.6. Finn punktet der drifta går i balanse og samanlikn med løysinga som du fann i oppgåve 2.6.
Eksempeloppgåve 2.9 Finn profittfunksjonen for bedrifra i oppgåve 2.5.
Løysing 2.5 Me har profittfunksjonen
som me kan forenkla til
Her er det greitt å fylgja mynsteret frå oppgåve 2.7:
| 50 | 25 | 50 | |
| 100 | 50 | 100 | |
| 200 | 250 | 200 | |
| 300 | 650 | 300 | |
| 400 | 1250 | 400 | |
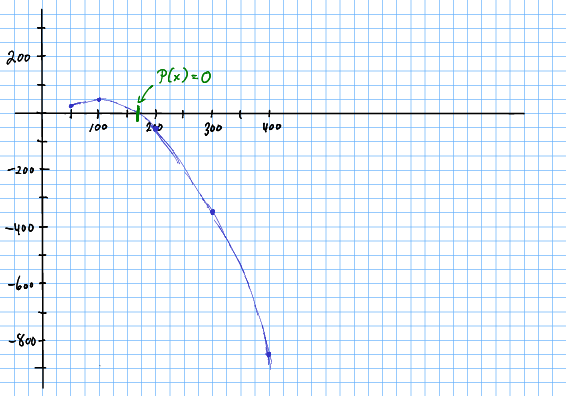
Me skal løysa likninga
Det er ofte meste behageleg å ha positiv fyrstegradskoeffisiet, so me gongar med på båe sider og får
som allereie har standardformen med , og , og formelen gjev
Me kan rekna ut dei ulike ledda og få
eller
Dette gjev to nullpunkt, og , men kostnadsfunksjonen føreset , so berre den siste løysinga er gyldig.
Ikkje berre finn me det same nullpunktet som i oppgåve 2.5, men me har løyst den eksakt same likninga på standardform. Nullpunktet (krysningspunktet med -aksen) i plottet ligg på som før.
Øvingsoppgåve 2.10 Finn profittfunksjonen for bedrifra i oppgåve 2.6.