Stigningstal og grensekostnaden

Eksempeloppgåve 3.1 Lat oss ta kostnadsfunksjonen

K (x) = x^{2} - x + 2 .

Me tenkjer oss at bedrifta sel (t.d.) mjøl i lausvekt. Når dei aukar produksjonen, so treng dei ikkje auka med ein heil kilo; dei kan auka med eit gram, eit milligram, eit mikrogram eller ein kvan lita storleik du kan tenkja deg.

1.: Plott $K (x)$ på intervallet $x = 0 \dots 8$ .
2.: Marker kostnaden for $x = 5$ på kurva.
3.: Marker kostnaden for $x = 6$ på kurva, og dra ei rett line gjennom kostnadene for $x = 5$ og $x = 6$ . Kva er stigningstalet på denne lina?
4.: Rekn ut kostnaden ved å auka produksjonen frå $x = 5$ til $x = 6$ .

Løysing 3.1 Me reknar ut $K (x)$ for $x = 0, 2, 4, 6, 8$ og markerer verdiane direkte i plottet, som under. Resten av plottet gjer me på frihand:

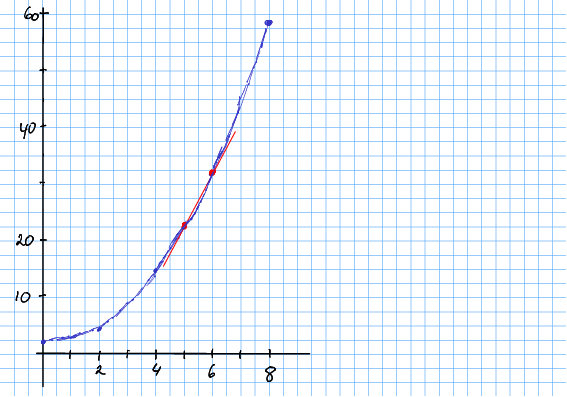
For å finna eksakt endringskostnad, må me setja inn tal og rekna, som fylgjer

\begin{align} K (5) & = 5^{2} - 5 + 2 = 22 & (11) \\ K (6) & = 6^{2} - 6 + 2 = 32 & (12) \\ Δ K = K (6) - K (5) & = 32 - 22 = 10 . & (13) \end{align}

Ekstrakostnaden når produksjonen aukar frå fem til seks einingar er ti.

Øvingsoppgåve 3.2 Lat oss ta kostnadsfunksjonen

K (x) = - \frac{x^{2}}{10} + 4 x + 1 .

Varane vert selde i lausvekt slik at $x$ kan ta vilkårlege verdiar, ikkje berre heiltalsverdiar.

1.: Plott $K (x)$ på intervallet $x = 0 \dots 8$ .
2.: Marker kostnaden for $x = 5$ på kurva.
3.: Marker kostnaden for $x = 6$ på kurva, og dra ei rett line gjennom kostnadene for $x = 5$ og $x = 6$ . Kva er stigningstalet på denne lina?
4.: Rekn ut kostnadauka $Δ K$ når produksjonen aukar frå $x = 5$ til $x = 6$ .

Merknad 3.1 (Delta) Den greske bokstaven $Δ$ (uttalt D på gresk) er hyppig brukt som symbol for endring i matematikken. Difor skriv me $Δ x$ for ei endring i $x$ og $Δ K$ for ei endring i $K (x)$ .

Merknad 3.2 (Kontinuerleg og diskret funksjon) I matematikken skil me gjerne mellom diskrete og kontinuerlege funksjonar. Ein diskret vare er ein vare som må teljast, t.d. klesplagg eller bilar. Ingen vil ha ein halv bil eller 0,1324 jakker. Andre varer vert målte kontinuerleg, t.d. øl (i liter) eller mjøl (i kilo).

Merknad 3.3 Mykje av matematikken som me lærer gjev berre meining for kontinuerlege funksjonar. Oppgåvene under gjev til dømes ikkje meining dersom bedrifta sel bilar. Når ein sel bilar er kostnadsfunksjonen $K (x)$ diskret, sidan $x$ må vera eit heiltal.

Det er likevel vanleg å tenkja kontinuerleg når ein løyser modeller, for so å tolka løysinga til slutt, med tanke på den diskrete røynda. Dette må ein tenkja på når ein bruker matematikk på praktiske problem.

Merknad 3.4 (Diskret tid) Renterekning er eit anna døme på diskrete funksjonar. Når rentene vert rekna ut periodevis, slik som er vanleg, vert tida i rentemodellen diskret. Tida vert tald i periodar, og ikkje målt i sekund.

Kontinuerleg forrenting er ei matematisk oppfinning for å unngå utfordringane med diskret tid.

Eksempeloppgåve 3.3 Me skal sjå vidare på kostnadsfunksjonen frå oppgåve 3.1:

K (x) = x^{2} - x + 2 .

1.: Plott $K (x)$ på intervallet $x = 0 \dots 6$ .
2.: Marker kostnaden for $x = 5$ på kurva.
3.: Marker kostnaden for $x = 5,2$ på kurva, og dra ei rett line gjennom kostnadene for $x = 5$ og $x = 5,2$ . Kva er stigningstalet på lina?
4.: Rekn ut ekstrakostnaden $Δ K$ ved å auka produksjonen frå $x = 5$ til $x = 5,2$ . Samanlikn med stigningstalet.

Løysing 3.2 Me teiknar plottet som me gjorde i forrige døme. Det er vanskeleg å sjå nøyaktig kva som skjer, so me teiknar ein versjon i større skala, der me berre tek med det interessante området. Då er det mogleg, so vidt, å sjå korleis lina krysser kurva to gongar.

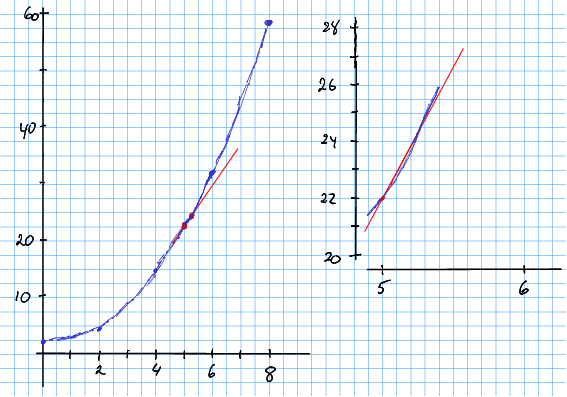
I figuren kan me sjå at lina gjennom dei to punkta har stigningstal om lag 9,2.

For å finna kostnadsauka, må me fyrst finna kostnaden i dei to punkta me er interesserte i. Då får me:

\begin{align} K (5) & = 5^{2} - 5 + 2 = 22 & (14) \\ K (5,2) & = {5,2}^{2} - 5,2 + 2 = 23,84 & (15) \\ K (5,2) - K (5) & = 23,84 - 22 = 1,84 . & (16) \end{align}

Det går an å sjå at stigningstalet er fem gongar kostnadsauka.

5 \cdot 1,84 = 9,2 .

Det heng saman med at produksjonsauka, frå 5 til 5,2, er på ein femtedels eining, eller 0,2. Stigningstalet skal då vera

\frac{1,84}{0,2} = 9,2,

som me såg stemmer.

Øvingsoppgåve 3.4 Me skal sjå vidare på kostnadsfunksjonen frå oppgåve 3.2:

K (x) = - \frac{x^{2}}{10} + 4 x + 1 .

1.: Plott $K (x)$ på intervallet $x = 0 \dots 6$ .
2.: Marker kostnaden for $x = 5$ på kurva.
3.: Marker kostnaden for $x = 5,2$ på kurva, og dra ei rett line gjennom kostnadene for $x = 5$ og $x = 5,2$ . Kva er stigningstalet på lina?
4.: Rekn ut kostnaden ved å auka produksjonen frå $x = 5$ til $x = 5,2$ . Samanlikn med stigningstalet.

Merknad 3.5 (Sekant) Dei rette linene som me har teikna i oppgåvene over vert kalla sekantar. Dei skjærer kurva i to punkt.

Merknad 3.6 Det gjeld generelt at stigningstalet åt sekanten er lik kostnadsauka per eining, når produksjonen aukar frå det eine til det andre skjæringspunktet på kurva. Når sekanten kryssar for produksjonsvoluma $x_{1}$ og $x_{2}$ , finn me altso stigningstalet som

a = \frac{Δ K}{Δ x} = \frac{K (x_{2}) - K (x_{1})}{x_{2} - x_{1}} .

Eksempeloppgåve 3.5 Me skal sjå vidare på kostnadsfunksjonen frå oppgåve 3.1 og 3.3:

K (x) = x^{2} - x + 2 .

Me skal studera kostnaden ved ørsmå produksjonsauker.

Ta utgangspunkt i produksjonsnivået $x = 5$ , og sjå på ulike produksjonsendringar $Δ x$ . Rekn ut kostnaden før ( $K (x)$ ) og etter ( $K (x + Δ x)$ ), samt endringa $Δ K = K (x + Δ x) - K (x)$ og den relative kostnadsauka per eining $Δ K ∕ Δ x$ .

Løysing 3.3 Det er enklast å setja dette opp i ein tabell. Me hugsar frå tidlegare oppgåver at $K (5) = 22$ .

$Δ x = x_{ny} - 5$	$x_{ny}$	$K (x_{ny})$	$Δ K = K (x_{ny}) - K (5)$	$\frac{Δ K}{Δ x}$
1	6	32	10	10
0,2	5,2	23,84	1,84	9,2
0,05	5,05	22,4525	0,4525	9,05
0,01	5,01	22,0901	0,0901	9,01
0,001	5,001	22,000 90	0,000 90	9,001
0,0001	5,0001	22,009 001	0,009 001	9,0001

Me ser at når $Δ x \to 0$ ,¹ vil $Δ K ∕ Δ x \to 9$ .

Øvingsoppgåve 3.6 Me skal sjå vidare på kostnadsfunksjonen frå oppgåve 3.2 og 3.4:

K (x) = - \frac{x^{2}}{10} + 4 x + 1 .

Me skal studera kostnaden ved ørsmå produksjonsauker.

Ta utgangspunkt i produksjonsnivået $x = 5$ , og sjå på ulike produksjonsendringar $Δ x$ . Rekn ut kostnaden før ( $K (x)$ ) og etter ( $K (x + Δ x)$ ), samt endringa $Δ K = K (x + Δ x) - K (x)$ og den relative kostnadsauka per eining $Δ K ∕ Δ x$ .

Merknad 3.7 (Tangent) I oppgåva over har me studert ein sekant som skjærer kostnadskurva for eit punkt $x$ og eit anna punkt $x + Δ x$ , for ei lita endring $Δ x$ . Når $Δ x \to 0$ nærmer sekanten seg ein tangent, som rører ved kurva i eitt punkt.

Merknad 3.8 Stigningstalet åt sekanten er

a = \frac{Δ K}{Δ x} = \frac{K (x + Δ x) - K (x)}{Δ x} .

Dersom me let $Δ x \to 0$ , vil $a$ nærma seg stigningstalet åt tangenten.

Merk at me ikkje kan setja $Δ x = 0$ , fordi me då deler på null. Likevel kan ein studera kva som skjer når $Δ x \to 0$ .

Merknad 3.9 Når me har ein funksjon og ein tangent som rører ved funksjonen for ein bestemt verdi av $x$ , so seier me at stigningstalet åt tangenten er den deriverte av funksjonen i punktet $x$ .

Grensekostnad

3.1 Stigningstal og grensekostnaden