Matematisering

Grensekostnad

Den deriverte som ein funksjon

3.2 Den deriverte som ein funksjon

I forrige avsnitt vart me kjende med den deriverte, stigningstalet på ei kurve som ikkje treng vera rak, i eit bestemt punkt. På ei krum kurve varierer stigningstal langs kurva. Når $f (x)$ er ein funksjon, skriv me gjerne $f^{'} (x)$ for stigningstalet. Sidan stigningstalet varierer med $x$ , er òg $f^{'} (x)$ ein funksjon.

Merknad 3.10 Den deriverte $f^{'} (x)$ kan me tenkja på som stigningstalet åt $f (x)$ , eller, for å vera pirkut, som stigningstalet åt ein tangent til kurva åt $f (x)$ i punktet $x$ .

Dersom $f (x)$ er ein kostnadsfunksjon, kallar me $f^{'} (x)$ for grensekostnaden.

Eksempeloppgåve 3.7 Lat oss sjå vidare på grensekostnaden for bedrifta i forrige avsnitt. Kostnadsfunksjonen var

K (x) = x^{2} - x + 2 .

Me skriv $K^{'} (x)$ for stigningstalet (grensekostnaden) åt $K (x)$ .

Bruk plottet som du har av $K (x)$ , og estimer stigningstalet $K^{'} (x)$ på augemål, for $x = 1, 2, 3, 4$ .

Løysing 3.4

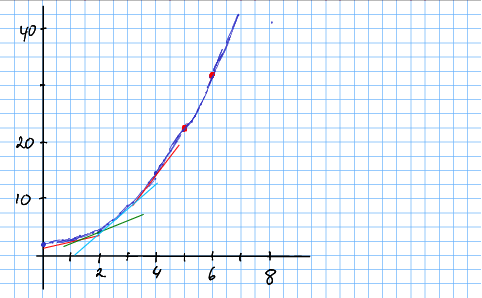
Tangenten for $x = 1$ (raud til venstre) ser ut til å stiga ei halv rute, eller 1,25, $x$ går frå 0 til 1. Det gjev eit stiningstal på litt meir enn 1.

Tangenten for $x = 2$ (grøn) stig cirka ei rute (2,5) når $x$ går frå 2 til 3. Det gjev eit stigningstal på $2,5$ .

Tangenten for $x = 3$ (cyan) stig nesten to ruter (5) når $x$ går frå 3 til 4. Det gjev eit stigningstal på mellom 4 og 5.

Tangenten for $x = 4$ (raud til høgre) ser ut til å stiga knapt tre ruter, eller 7,5, $x$ går frå 3,5 til 4,5. Det gjev eit stiningstal på vel 7.

Øvingsoppgåve 3.8 Sjå på plottet som du har av kostnadsfunksjonen

K (x) = - \frac{x^{2}}{10} + 4 x + 1

frå forrige avsnitt. Estimer stigningstalet $K^{'} (x)$ på augemål, for $x = 1, 2, 3, 4$ .

Lat $f (x) = a x^{2} + b x + c$ vera ein kvadratisk funksjon. Då er den deriverte gjeven som

f^{'} (x) = a \cdot 2 \cdot x + b

Rekneregel 3.1: Rekneregel: Derivasjon av kvadratisk funksjon.

Eksempeloppgåve 3.9 Me har

K (x) = x^{2} - x + 2 .

Finn eit uttrykk for grensekostnaden $K^{'} (x)$ ved hjelp av formelen i rekneregel 3.1. Rekn ut $K^{'} (x)$ for $x = 1, 2, 3, 4$ og samanlink med estimata dine frå oppgåve 3.7.

Løysing 3.5 Formelen gjev

K^{'} (x) = 2 x - 1 .

Når me set inn, får me

\begin{align} K^{'} (1) = 2 \cdot 1 - 1 = 1, & (17) \\ K^{'} (2) = 2 \cdot 2 - 1 = 3, & (18) \\ K^{'} (3) = 2 \cdot 3 - 1 = 5, & (19) \\ K^{'} (4) = 2 \cdot 4 - 1 = 7 . & (20) \end{align}

Estimata våre i oppgåve 3.7 ligg stort sett nær dei sanne verdiane som me no har rekna ut. Den største bommen hadde me for $x = 2$ , men me ser òg at kurva var ujamnt teikna rundt dette punktet, so det er ikkje rart at tangenten òg vart litt feil.

Øvingsoppgåve 3.10 Me har

K (x) = - \frac{x^{2}}{10} + 4 x + 1

Finn eit uttrykk for grensekostnaden $K^{'} (x)$ ved hjelp av formelen i rekneregel 3.1. Rekn ut $K^{'} (x)$ for $x = 1, 2, 3, 4$ og samanlink med estimata dine frå oppgåve 3.8.

Eksempeloppgåve 3.11 Tenk deg at bedrifta, som har kostnadsfuknsjonen

K (x) = x^{2} - x + 2,

produserte $x = 4$ einingar i fjor. Kva må prisen vera for at det skal løna seg å auka produksjonen i år? (Bruk svara dine frå oppgåve 3.9 som mellomrekning.)

Løysing 3.6 Grensekostnaden gjev kostnadsauka for ei lita (marginal) auke i produksjonen. For å tena pengar, må prisen dekkja denne kostnaden. Me fann $K^{'} (4) = 7$ , og me treng difor ein pris større enn sju.

Øvingsoppgåve 3.12 Tenk deg at bedrifta, som har kostnadsfuknsjonen

K (x) = - \frac{x^{2}}{10} + 4 x + 1

produserte $x = 4$ einingar i fjor. Kva må prisen vera for at det skal løna seg å auka produksjonen i år? (Bruk svara dine frå oppgåve 3.10 som mellomrekning.)